What is "Modified Declination"?

         At many web pages, which deal with how to align a TVRO satellite system, either a big C-band system or smaller Ku only system, you will see instructions which suggest that you should set your main rotation axis of your mount parallel to the earth's rotation axis, and then they give you a chart or calculator which then gives you a "DECLINATION" angle that your dish should aim below the plane perpindicular to this axis.   This is basically the same as setting your mount so that the rotation axis of the motor or mount is at an angle equal to your latitude relative to the ground, and that the plane perpindicular to this axis is at an angle of (90-latitude) with respect to the southern horizon.  These web pages usually calculate declination angles that are the declination angle for a satellite to your south.

  However SOME web pages, such as mine, recommend using something called "Modified Declination", so often the question comes up as to just what is this modified declination?   One good web page where you can get some good information about modified declination is the

GEO-ORBIT declination charts     

You will see at that page, declination charts, which differ slightly, usually by about 0.6 degrees for medium latitudes.  The difference between these two charts is that the regular declination charts were calculated for sats to your south, while the modified declination is calculated for sats to your east or western horizon.  East or West declinations are slightly smaller, because you are further away from these sats, so you don't have to look so far down to see the Clarke belt. 

See the calculator at:  http://www.eskerridge.com/bj/sat/bjdishcalc2.htm   At the top of this calculator, you can calculate your declination to southern sats and to east/west sats, so you can see how they differ.

Below, is a sketch that tries to explain what declination is, and how it's calculated. 


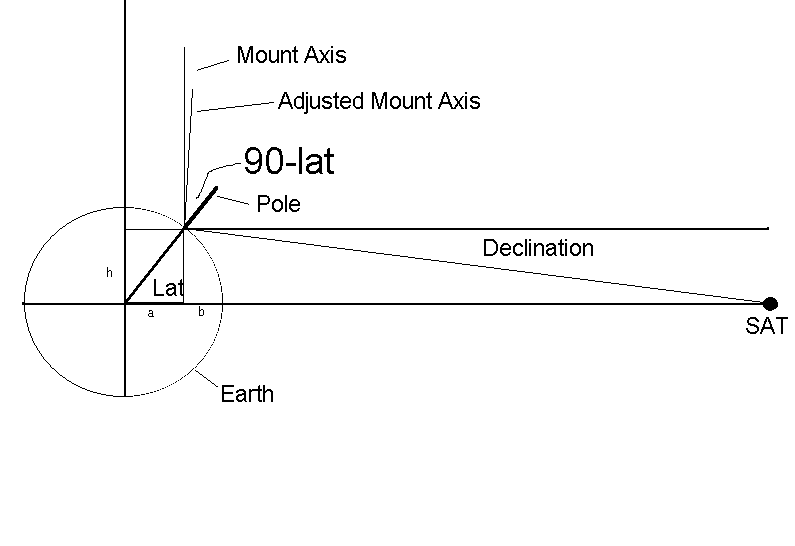
Above, "h" and "a" are  sin(lat) and cos(lat) respectively times the radius of the earth, and "b" is the radius minus a.  Then, the distance to the sat along the equatorial plane is b plus the published 22,236 mile height of the geostationary orbit, which we can call "c".  The declination is then the arctan(h/(b+c)).   This declination, however is only the declination of a sat to your true south.  Sats to your east or west are further away, by up to an additional "a" amount, so somehow we need to figure out how to track the arc when the declination needed to follow the arc is different for each satellite.


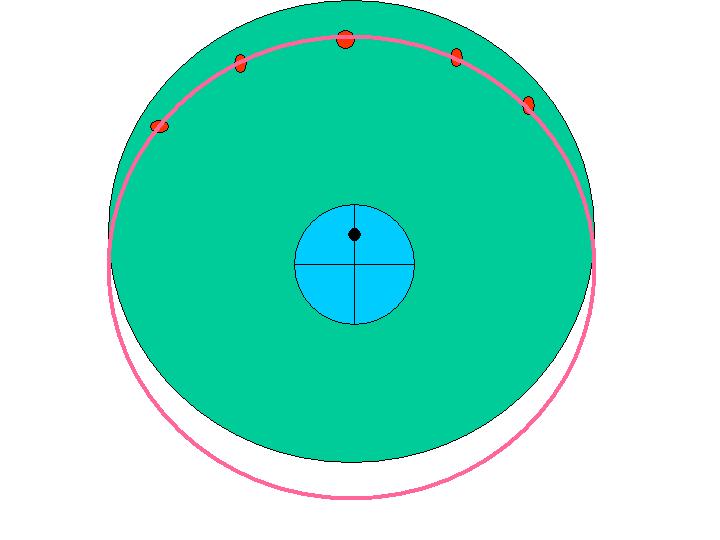
To explain what declination does, imagine that you are at the north pole.  Since the satellites are in a plane defined by the equator, you have to look down by an angle called declination in order to aim at the satellites. {Actually you can't see geostationary satellites from the north pole, but if you could, the diagram below is what it would look like. Note, the blue circle is supposed to be the earth, and the little red circles are supposed to be the satellites.   You need to look down via a declination angle to see the sats in the equatorial plane.  The shape swept out by your dish when it rotates is actually a CONE shape when you have declination.  If you didn't have declination, the dish would sweep out a horizontal plane way above the equatorial plane described by the yellow in the image below (this is a plane, not a line as shown in the image. Also see the horizontal line above the word declination in the sketch above, which represents the dish aime without declination.



      

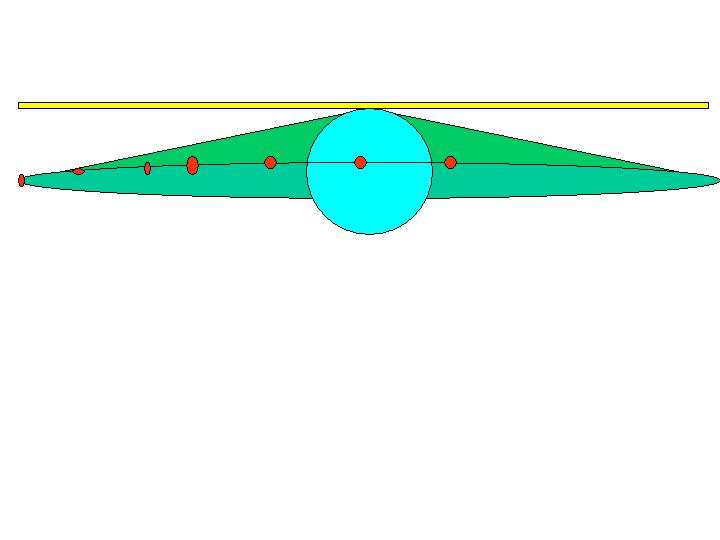
The view from above the north pole would look like the following diagram.     Assuming that you could see the sats from the north pole, the north pole would be the ONLY place on earth where the circular cone would hit all the sats perfectly.  Again, the blue circle is the earth, and we're centered on the north pole.                 
                                                 
                                                                 
                                                                   
 
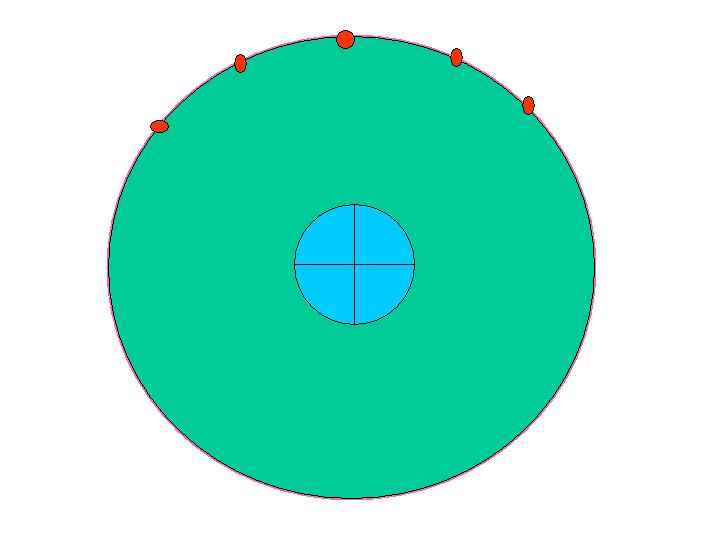
Now, lets move down to some medium latitude instead of showing the view from the north pole.  This is shown below.   You will see that the green circle is smaller because the declination is smaller as the latitude gets smaller.  The problem, however, is that the circle defined by the declination cone does not hit the sats to the east or west of the sat dish location, because the declination of those sats is smaller than the declination of sats to your south, since the sats to your south are closer to you.  The error can be up to about 1/2 degrees on sats to your east or west.





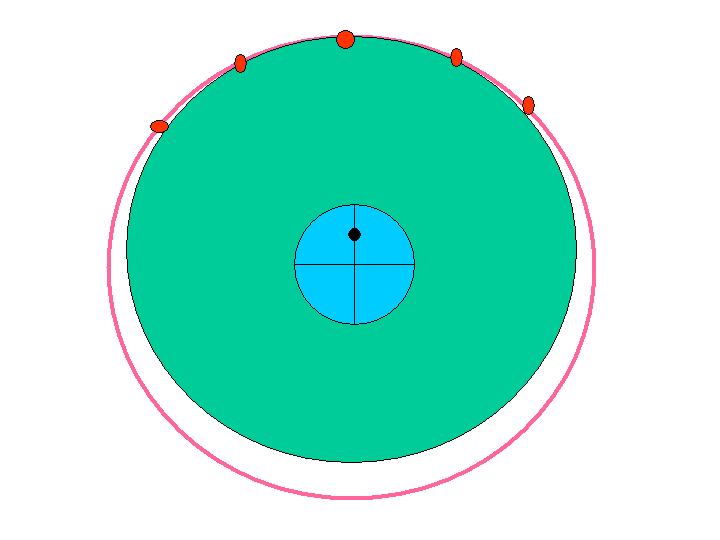
In order to hit the sats to your east or west, it is necessary to use the declination of an easterly or westerly satellite.  However you see the problem when you do this, is that the cone defined by this declination will not hit sats to your south.  It only hits the arc to your extreme east/west, and you'd be off by up to 1/2 deg on your south sat.





The solution is to tip the motor elevation down slightly (by approximately 1/2 degrees) toward your southern horizon.  This tilts the cone you're sweeping out, so that the projection of the cone shape describes an elipse where it intercects the equatorial plane, instead of a circle.  You see below how this results in you being able to track the arc nearly perfectly, within a couple hundredths of a degree.   You notice that when you tilt the motor elevation, it doesn't change the reception of east/west sats, it only changes the southerly component of your aim, and it's change is proportional across the arc, ie more to the south and less to the east/west. 



{To be more accurate, the above elipse analogy doesn't really represent where an extended cone intercects the equatorial plane, which is why I used the projection term above, and I was referring to assuming that the cone was finite at the distance down to the equatorial plane.  This would result in the easy to understand eliptical projection. In reality though, the arc swept by the actual intercection of the extended cone would be wider than the orbital circle at the bottom.  I know that's confusing, which is why I used the eliptical explanation, but I thought I should explain that it wasn't quite accurate.}

But the important concept is that by tilting the axis forward, it corrects for the  1/2 degree error on the south sats, and the correction does not affect east or west sats at all, and is applied proportionally on the intermediate sats, so that tracking is accurate to at least a couple hundredths of a degree.